[Maya][Rig]3本以上の骨のIK

現在弊社では、Autodesk Maya で動作する新しいリグシステムの開発を行っております。この開発の中で、標準機能に無いIKのアルゴリズムをいくつか実装しましたので３つほどご紹介いたします。「こんなIKがあるんだな」「こんな動き方をするんだな」と思っていただければいいなと思います。

3本以上の骨のIK

1本または2本の骨に対するIKは、ターゲット（拘束位置、到達点）やアップベクトルによって骨の角度が定まるため、どのようなアルゴリズムでも結果はほとんど変わりません。ところが、3本以上の骨となるとあらゆる状態が解として存在します。

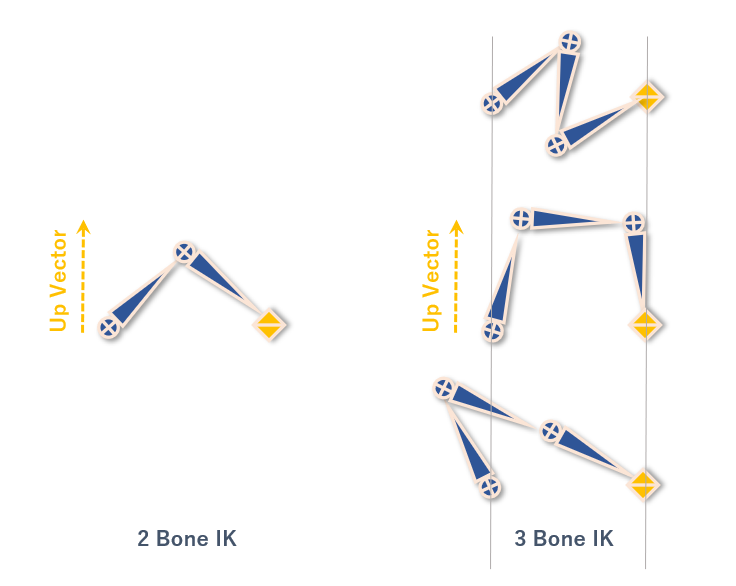
Mayaの標準IKソルバにとらわれず、リグを操作するアニメーターさんにとって直感的で安心して制御できる方法を見つけたいと思ったのが、各アルゴリズムの実装検証を開始したきっかけです。

NCF-IK (Non-Iterative, Closed-form, Inverse Kinematic Chain Solver)

CCD-IKやParticle-IKのような反復計算による収束は行わず、各関節ごとに三角関数で一発で解を導きます。この手法は「Game Programming Gems 8」の中で紹介されています。この本に収録されているCDには、動作の確認ができる実行ファイルやソースコードが含まれているため大変参考になります。

Game Programming Gems 8 | CGWORLD SHOP https://shop.cgworld.jp/shopdetail/000000000245/

以下の動画は、NCF-IK（水色）とMayaのIKソルバ（黄色）で比較したものです。IKのルートとターゲットの距離が近いとき、Maya標準ソルバでは不安定な挙動になっていますがNCF-IKは非常に安定しているのが分かります。

FABRIK (Forward And Backward Reaching inverse kinematics)

各関節の位置をベクトルの正規化とベクトルのスカラー乗算だけで移動させながら収束計算を行います。反復方法に特徴があり、A、B、Cという３本の骨があった場合、A→B→C→A→B→C…とはならず、FABRIKはA→B→C→C→B→A…のように往復します。

FABRIKについては、ほげたつ氏の以下の書籍を参考にいたしました。
画像付きで分かりやすいのでおススメです。
「実行時アニメーション制御: Runtime Animation Control」

また、動画の中にはないですが角度制限や球とのコリジョン機能なども実装テストしました。

Spline Curve IK (Catmull-Rom)

Catmull-Rom という曲線アルゴリズムを利用し、その曲線に対して骨を這わせる手法です。Catmull-Rom Spline曲線は、制御点を必ず通るという特徴があり「直感的」な操作が可能です。Mayaには標準機能としてNURBSカーブを使ったSplineIKソルバがありますが、NURBSカーブは制御点を通らないためリグとしては使いにくいときがたまにあります。また、Mayaには制御点を通るカーブとしてBezierカーブがありますが、Bezierカーブは制御点以外にタンジェントがあるため、リグとして考えると制御にやや難があります。

参考サイト：
　・Catmull-Romスプライン曲線 http://naochang.me/?p=1119
　・エルミート曲線 (Hermite Curve) http://naochang.me/?p=975

発展形としてHermite曲線上にCatmull-Rom Splineを這わせて、さらに制御点に簡易的なコリジョン処理および制御点同士の間隔補正を実装した例もご紹介します。

以上、簡単ではありますが３つのIKについてご紹介いたしました。

Archive

© TA inc.